Dans cette deuxième partie de notre analyse plus approfondie du rendu de jeu en 3D, nous allons nous concentrer sur ce qui se passe dans le monde 3D une fois que tous les traitements de vertex sont terminés. Nous devrons à nouveau dépoussiérer nos manuels de mathématiques, nous attaquer à la géométrie des troncs et réfléchir au puzzle des perspectives. Nous allons également plonger rapidement dans la physique du traçage des rayons, de l'éclairage et des matériaux – excellente!
Le sujet principal de cet article concerne une étape importante du rendu, où un monde tridimensionnel de points, de lignes et de triangles se transforme en une grille bidimensionnelle de blocs colorés. C’est vraiment quelque chose qui «se passe», car les processus impliqués dans la modification 3D-2D se déroulent de manière invisible, contrairement à notre article précédent où nous pouvions immédiatement voir les effets des vertex shaders et des tessellations. Si vous n'êtes pas prêt pour tout cela, ne vous inquiétez pas – vous pouvez commencer à utiliser notre 3D Rendu de jeu 3D 101. Mais une fois que vous êtes prêt, lisez la suite pour en savoir plus sur le monde des graphiques 3D.
Se préparer pour 2 dimensions
La grande majorité d'entre vous consultera ce site Web sur un écran totalement plat ou un écran de smartphone; Même si vous êtes cool avec les enfants et que vous avez un moniteur incurvé sophistiqué, les images qu’il affiche sont constituées d’une grille plate de pixels colorés. Et pourtant, lorsque vous jouez au dernier numéro de Call of Mario: Deathduty Battleyard, les images semblent être en 3 dimensions. Les objets entrent et sortent de l'environnement, deviennent plus grands ou plus petits, à mesure qu'ils se déplacent vers et depuis la caméra.
En utilisant l'exemple de Bethesda Fallout 4 de 2014, nous pouvons facilement voir comment les sommets ont été traités pour créer la sensation de profondeur et de distance, en particulier s'ils sont exécutés en mode filaire (ci-dessus).
Si vous choisissez un jeu 3D d’aujourd’hui ou des deux dernières décennies, presque chacun d’entre eux effectuera la même séquence d’événements pour convertir le monde 3D des sommets en un tableau 2D de pixels. Le nom du processus qui effectue le changement est souvent appelé rastérisation mais ce n'est qu'une des nombreuses étapes de tout le shebang.
Nous devrons décomposer quelques étapes et examiner les techniques et les mathématiques utilisées. Pour référence, nous utiliserons la séquence utilisée par Direct3D pour analyser ce qui se passe. L'image ci-dessous montre ce qui est fait pour chaque sommet du monde:
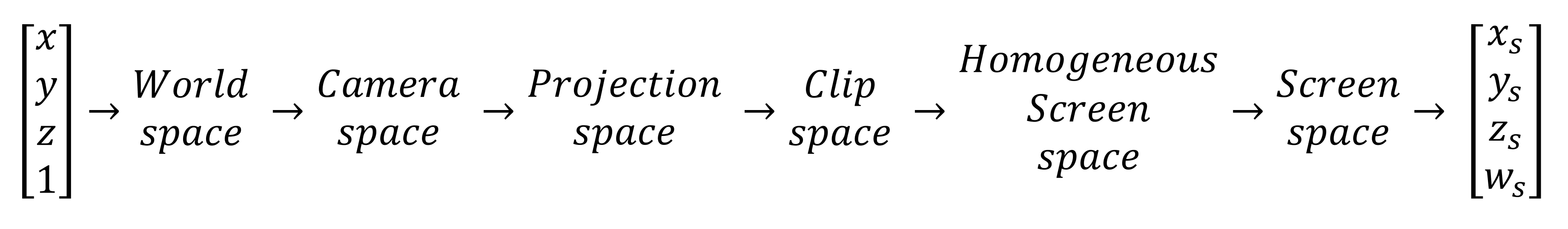
Nous avons vu ce qui a été fait sur la scène spatiale mondiale dans notre article de la partie 1: ici, les sommets sont transformés et colorés à l’aide de nombreux calculs matriciels. Nous ignorerons la section suivante car tout ce qui se passe dans l'espace de la caméra, c'est que les sommets transformés sont ajustés après leur déplacement afin de faire de la caméra le point de référence.
Toutefois, les étapes suivantes sont trop importantes pour être ignorées, car elles sont absolument essentielles pour passer de la 3D à la 2D – faites correctement -, et notre cerveau va regarder un écran plat mais "voir" une scène qui a une profondeur et une ampleur – – mal fait, et les choses vont avoir l'air très bizarre!
Tout est une question de perspective
La première étape de cette séquence consiste à définir le champ de vision, tel que vu par la caméra. Ceci est fait en commençant par définir les angles pour les champs de vision horizontal et vertical – le premier peut souvent être changé dans les jeux, car les humains ont une meilleure vision périphérique d'un côté à l'autre que de haut en bas.
Nous pouvons avoir une idée de cela à partir de cette image qui montre le champ de la vision humaine:
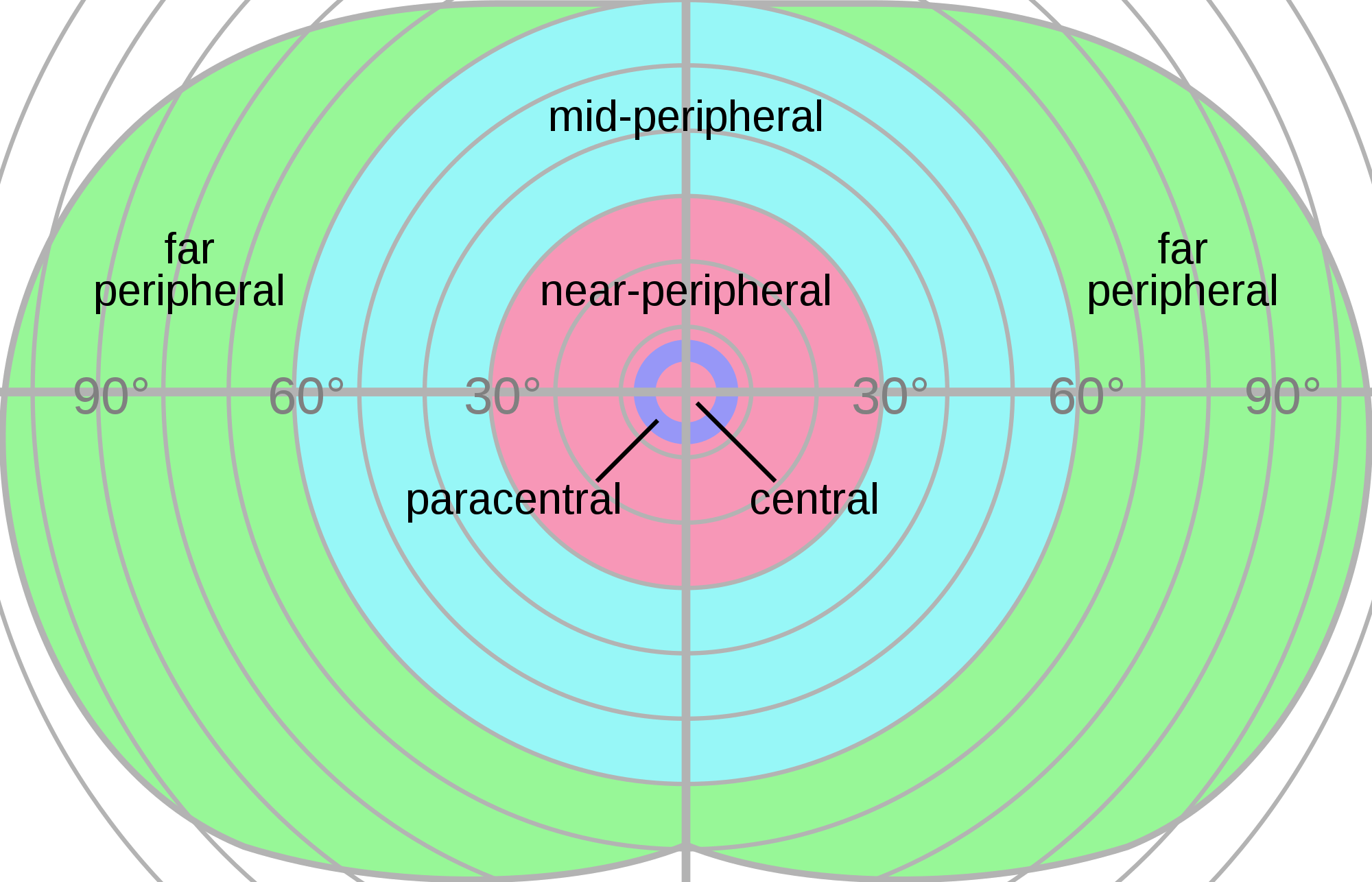
Les deux angles de champ de vision (fov, en abrégé) définissent la forme d’un frustum – une pyramide 3D à base carrée, qui émane de la caméra. Le premier angle est pour le verticale fov, le second étant le horizontal un; nous allons utiliser les symboles α et β pour les dénoter. Nous ne voyons pas tout à fait le monde de cette manière, mais il est beaucoup plus facile, d’un point de vue calcul, de calculer un frustum que de tenter de générer un volume de vues réaliste.
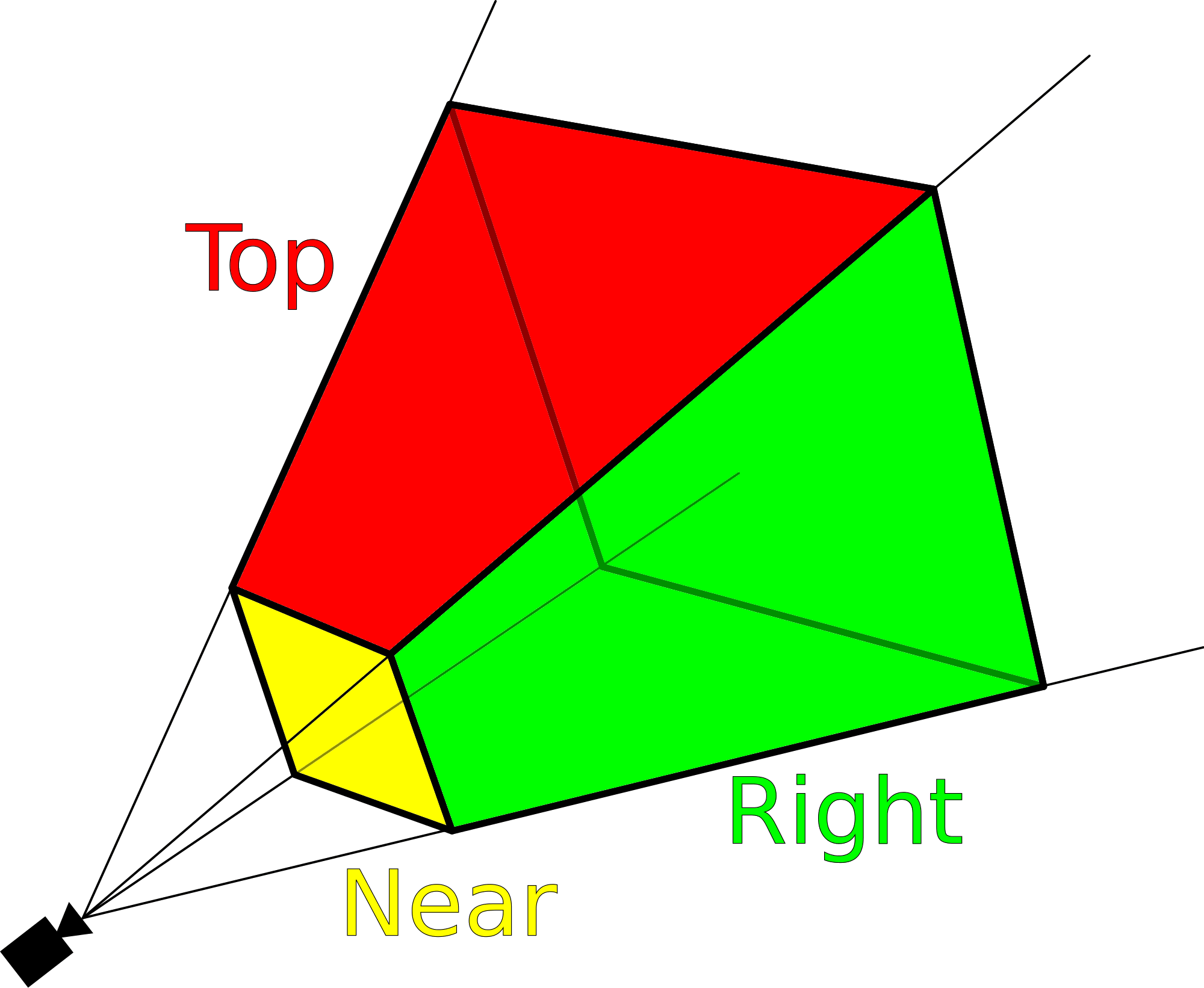
Deux autres paramètres doivent également être définis – la position du proche (ou du devant) et du loin (le dos) plans de découpage. La première tranche du haut de la pyramide, mais détermine essentiellement la proximité de la position de la caméra; le dernier fait de même mais définit à quelle distance de la caméra les primitives vont être rendues.
La taille et la position du plan de découpage proche sont importantes car elles deviennent ce que l’on appelle le fenêtre d'affichage. C’est essentiellement ce que vous voyez sur le moniteur, c’est-à-dire le cadre rendu, et dans la plupart des API graphiques, la fenêtre de visualisation est "dessinée" à partir de son coin supérieur gauche. Dans l'image ci-dessous, le point (a1, b2) serait l'origine du plan, et la largeur et la hauteur du plan sont mesurées à partir d'ici.
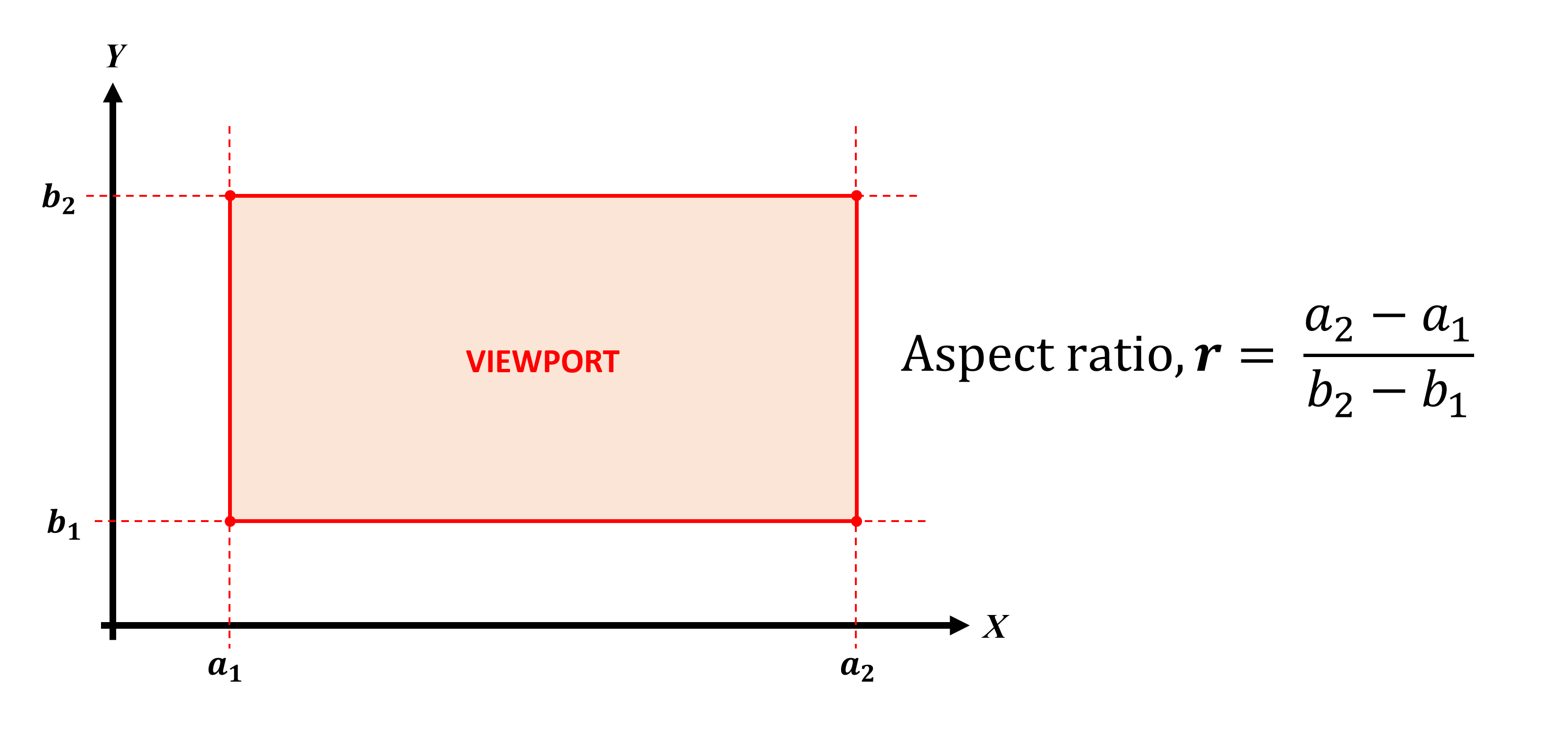
le ratio d'aspect L’aspect de la fenêtre de visualisation est non seulement déterminant pour l’apparence du monde affiché, mais il doit également correspondre au rapport hauteur / largeur du moniteur. Pendant de nombreuses années, cela a toujours été 4: 3 (ou 1,3333 … sous forme décimale). Aujourd'hui, cependant, beaucoup d’entre nous jouent avec des ratios tels que 16: 9 ou 21: 9, c’est-à-dire écran large et écran ultra large.
Les coordonnées de chaque sommet dans l'espace de la caméra doivent être transformées afin qu'elles s'adaptent toutes au plan de découpage proche, comme indiqué ci-dessous:
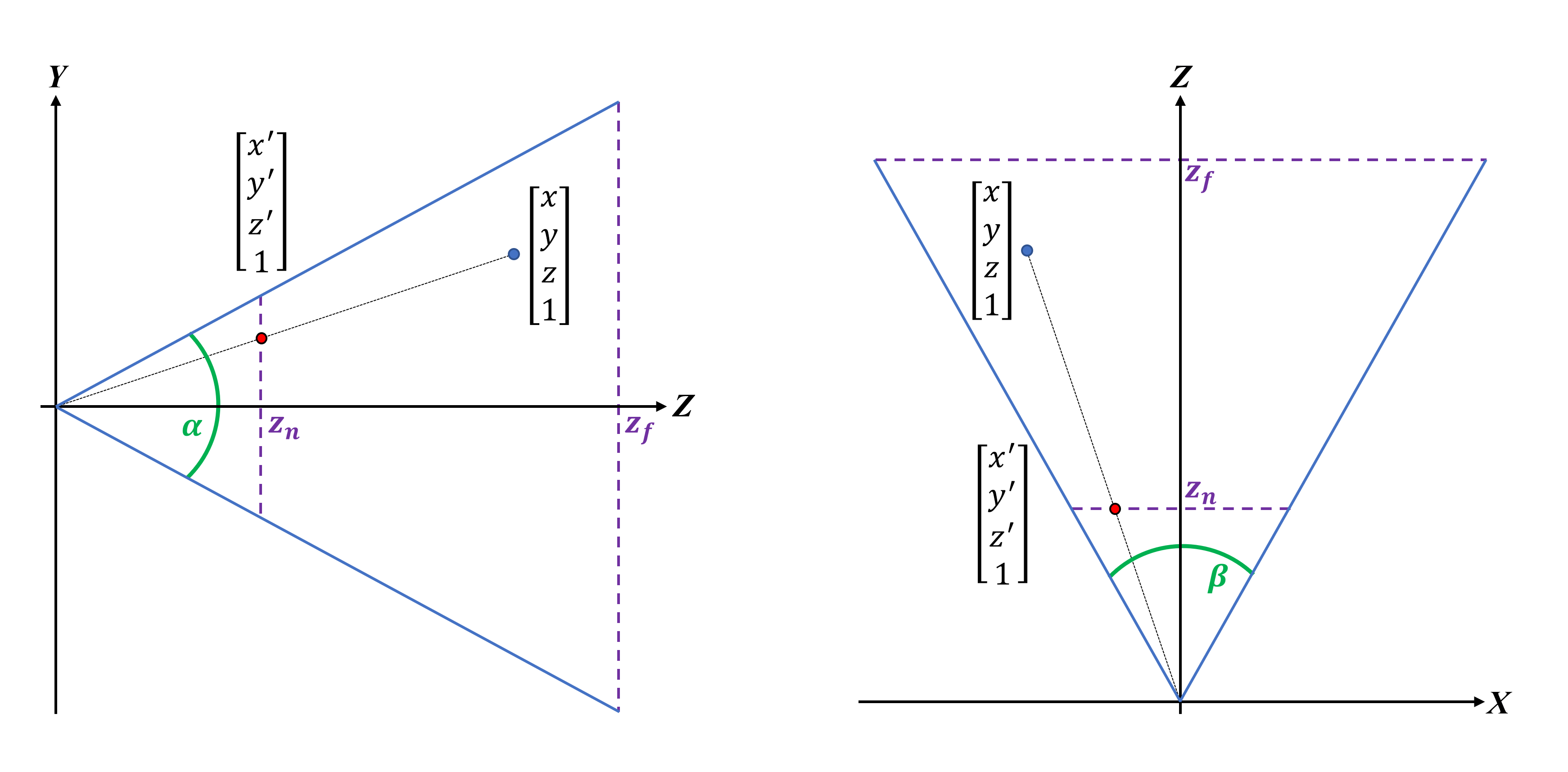
La transformation est effectuée en utilisant une autre matrice – celle-ci est appelée la matrice de projection en perspective. Dans notre exemple ci-dessous, nous utilisons les angles de champ de vision et les positions des plans de découpage pour effectuer la transformation. nous pourrions utiliser les dimensions de la fenêtre à la place.
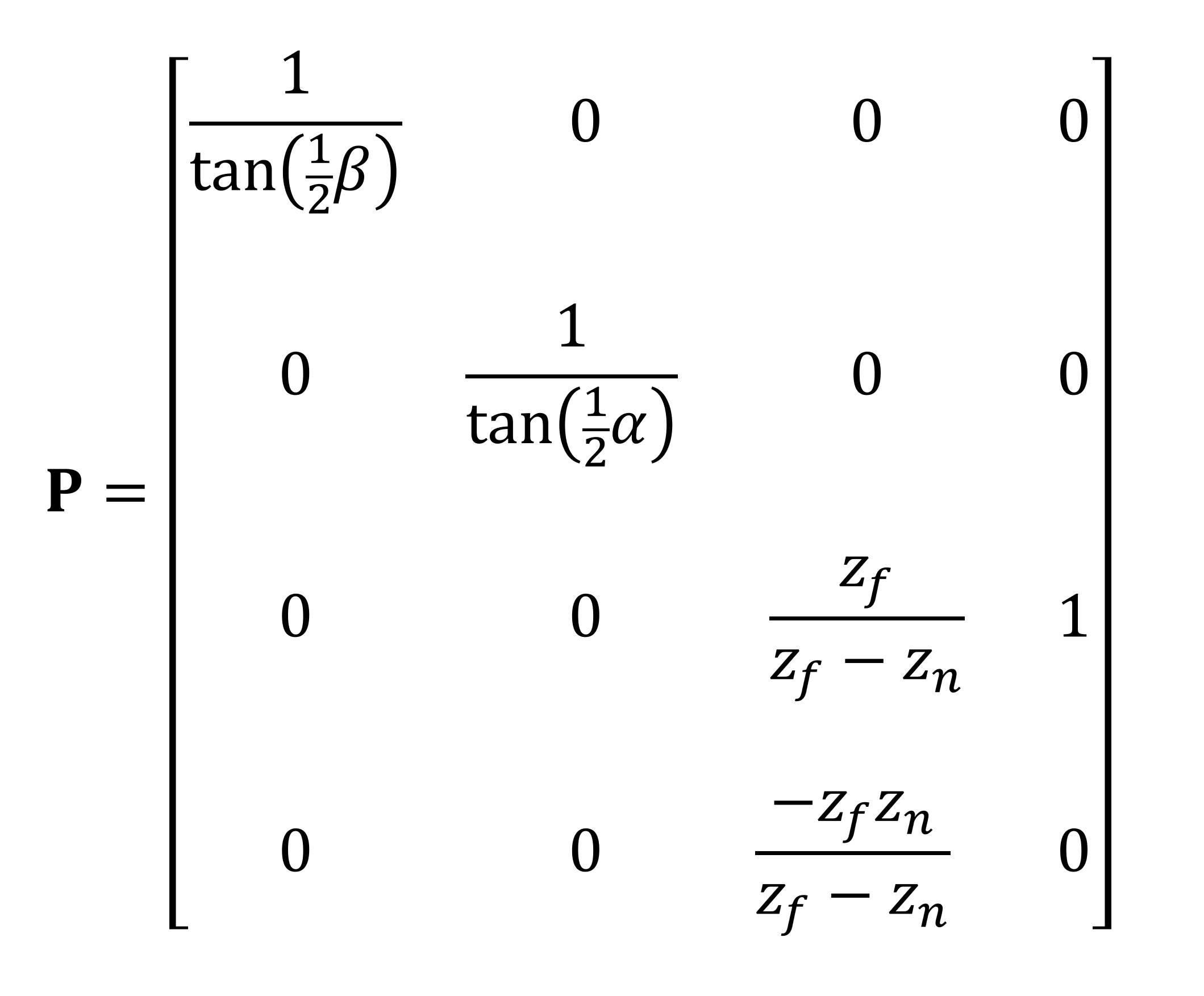
Le vecteur de position de sommet est multiplié par cette matrice, ce qui donne un nouvel ensemble de coordonnées transformées.
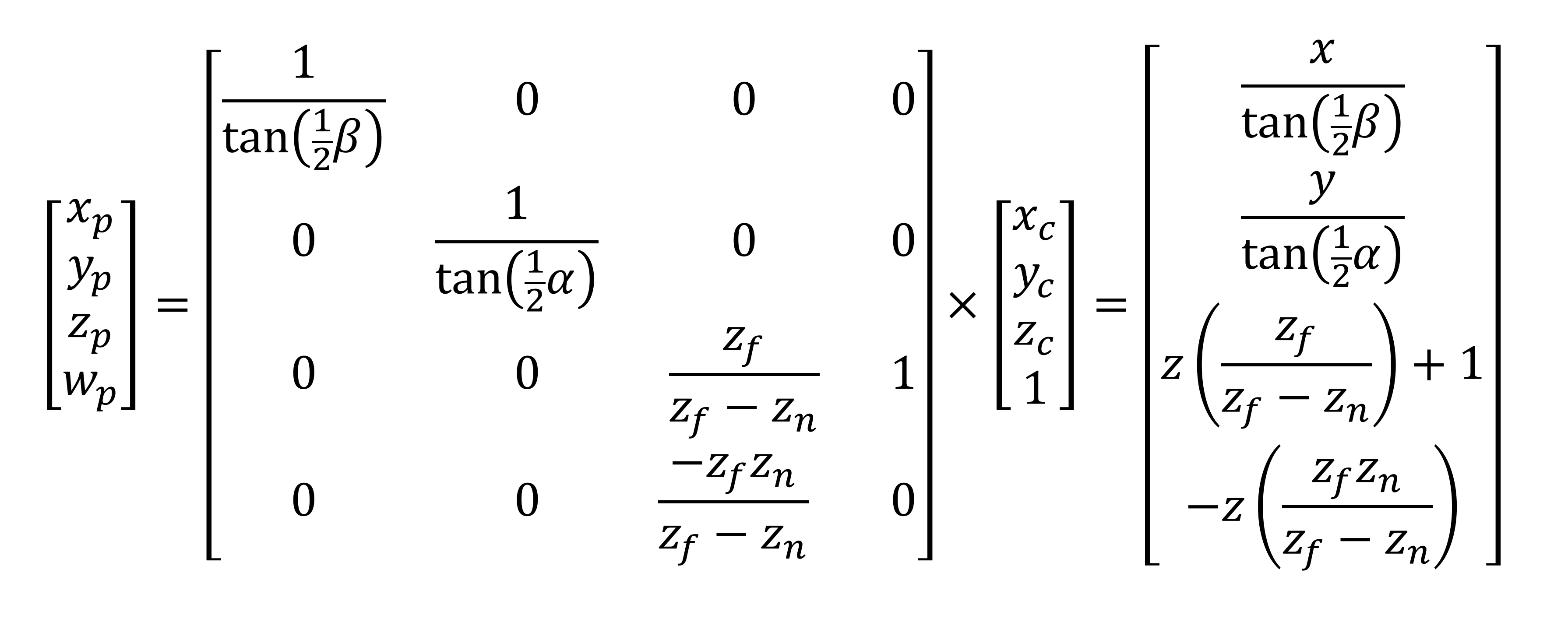
Et voilà! Tous nos sommets ont maintenant été écrits de telle manière que le monde d'origine apparaisse maintenant comme une perspective 3D forcée. Ainsi, les primitives proches du plan de découpe avant apparaissent plus grandes que celles situées plus près du plan distant.
Bien que la taille de la fenêtre d'affichage et les angles de champ de vision soient liés, ils peuvent être traités séparément. En d'autres termes, vous pouvez définir le tronc commun pour vous donner un plan de découpage presque différent en taille et en format par rapport à la fenêtre d'affichage. Pour que cela se produise, une étape supplémentaire est requise dans la chaîne, où les sommets du plan de découpage proche doivent être à nouveau transformés, afin de prendre en compte la différence.
Cependant, cela peut entraîner une distorsion dans la perspective vue. Skyrim, le jeu de Bethesda en 2011, nous permet de voir comment ajuster l'angle de champ de vision horizontal β, tout en conservant le même format d’aspect de la fenêtre, a un effet significatif sur la scène:

Dans cette première image, nous avons défini β = 75 ° et la scène semble parfaitement normale. Maintenant essayons avec β = 120 °:
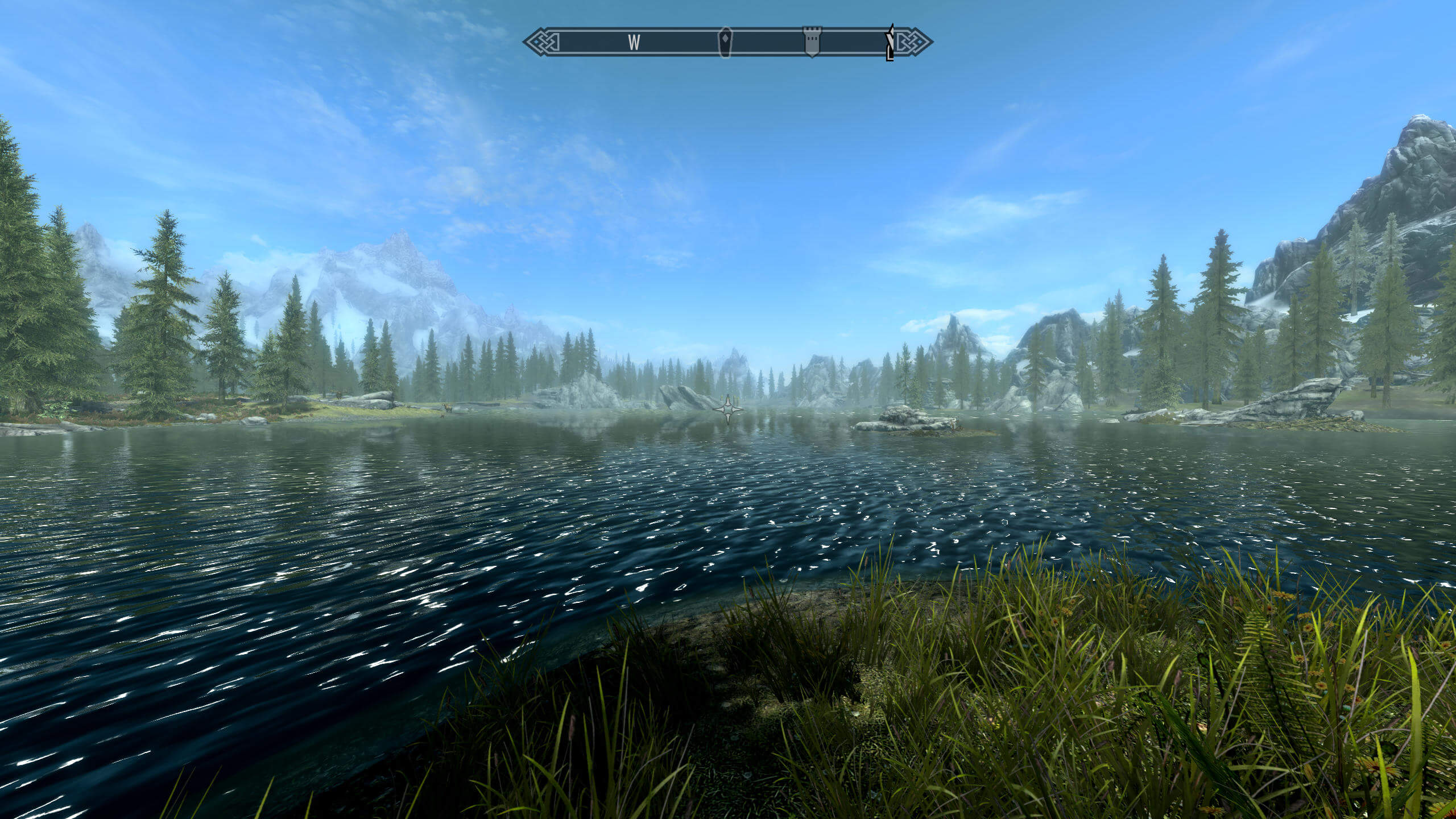
Deux différences sont immédiatement évidentes: premièrement, nous pouvons voir beaucoup plus de choses sur les côtés de notre vision et deuxièmement, les objets semblent maintenant beaucoup plus éloignés (les arbres en particulier). Cependant, l’effet visuel de la surface de l’eau n’a pas l’air actuel, c’est que le processus n’a pas été conçu pour ce champ de vision.
Supposons maintenant que notre personnage a les yeux comme des extraterrestres et β = 180 °!
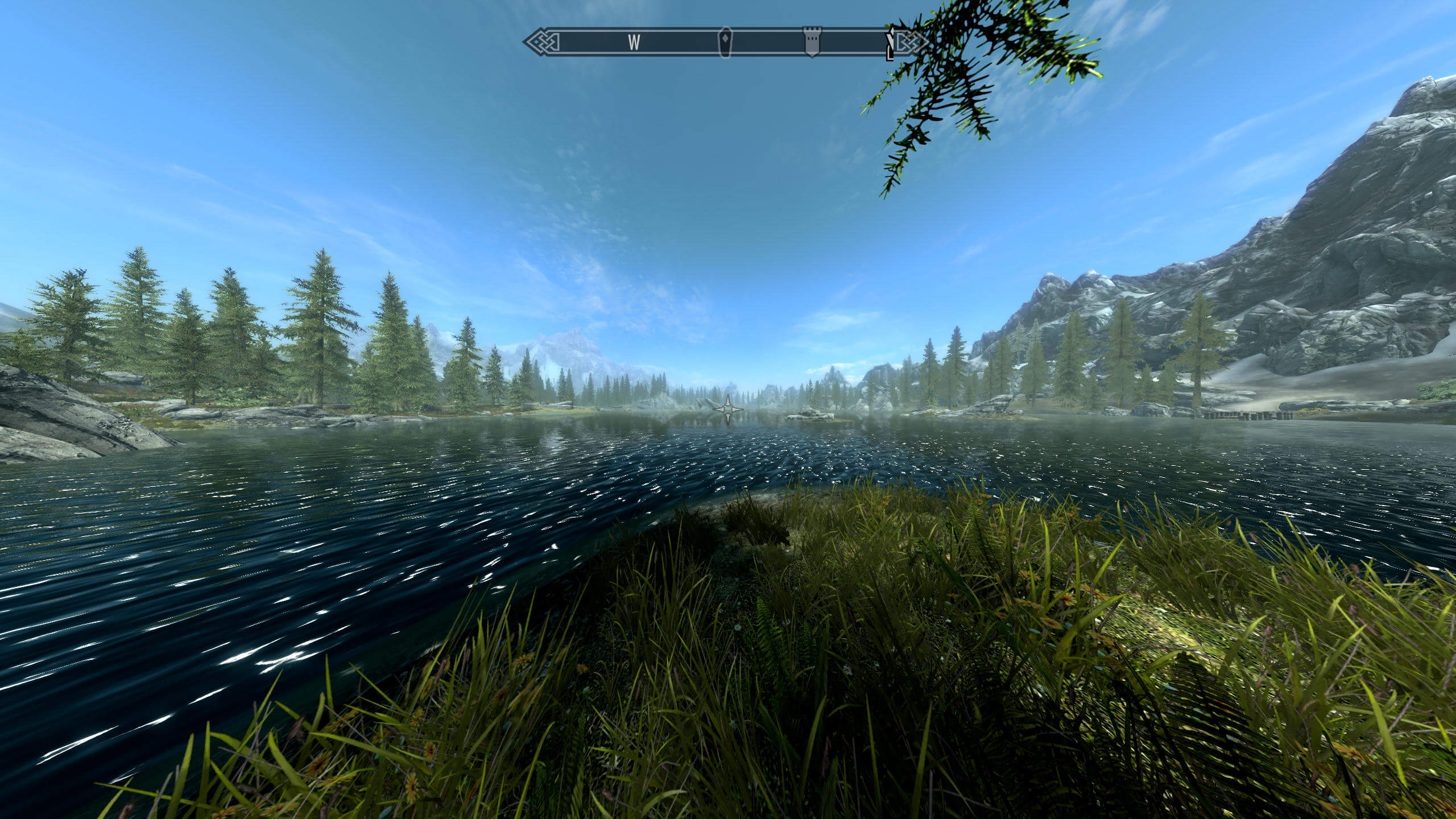
Ce champ de vision nous donne une scène presque panoramique mais au prix d'une grave distorsion des objets restitués sur les bords de la vue. Encore une fois, c'est parce que les concepteurs de jeux n'ont pas planifié et créé les ressources et les effets visuels du jeu pour cet angle de vue (la valeur par défaut est d'environ 70 °).
On pourrait croire que la caméra a bougé dans les images ci-dessus, mais ce n’est pas le cas; tout ce qui s’est passé est que la forme du tronc a été modifiée, ce qui a redéfini les dimensions du plan de découpage proche. Dans chaque image, les proportions de la fenêtre sont restées les mêmes. Une matrice de mise à l’échelle a donc été appliquée aux sommets pour que tout soit ajusté.
Alors, es-tu dedans ou dehors?
Une fois que tout a été correctement transformé dans la phase de projection, nous passons ensuite à ce qu'on appelle espace de clip. Bien que cela soit fait après projection, il est plus facile de visualiser ce qui se passe si on le fait avant:
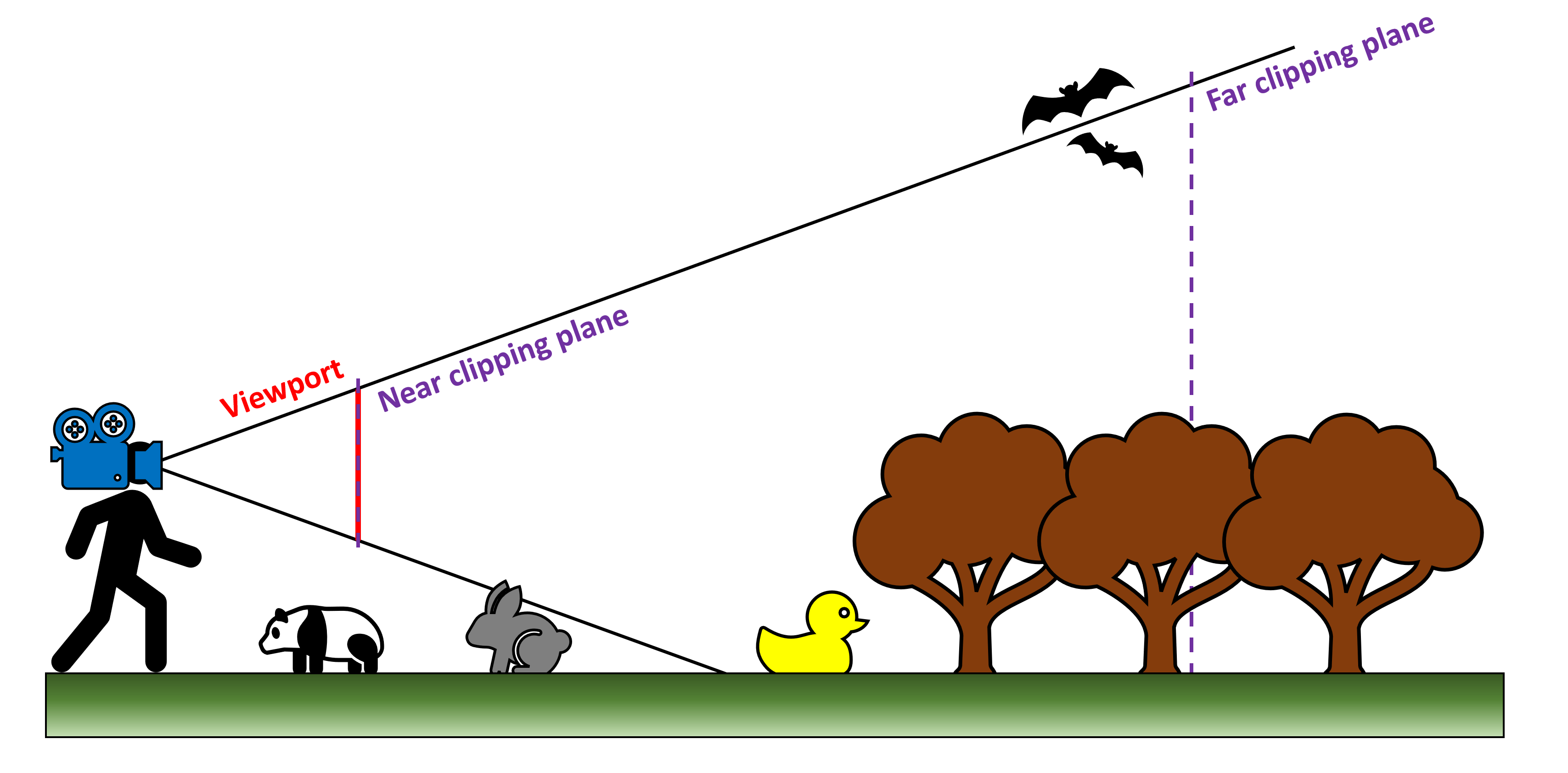
Dans notre diagramme ci-dessus, nous pouvons voir que le canard en caoutchouc, une des chauves-souris et certains des arbres auront des triangles à l'intérieur du tronc; cependant, l'autre chauve-souris, l'arbre le plus éloigné et le panda sont tous à l'extérieur du tronc. Bien que les sommets constituant ces objets aient déjà été traités, ils ne seront pas visibles dans la fenêtre d'affichage. Cela signifie qu'ils obtiennent coupé.
Dans coupure frustique, toutes les primitives situées en dehors du tronc sont entièrement supprimées et celles qui se trouvent sur n’importe laquelle des limites sont transformées en nouvelles primitives. Le découpage n'est pas vraiment un gain de performances, car tous les sommets non visibles ont été passés par des sommets de sommets, etc. L'étape de découpage elle-même peut également être ignorée, si nécessaire, mais cela n'est pas pris en charge par toutes les API (par exemple, OpenGL standard ne vous laissera pas ignorer, alors qu'il est possible de le faire en utilisant une extension API). .
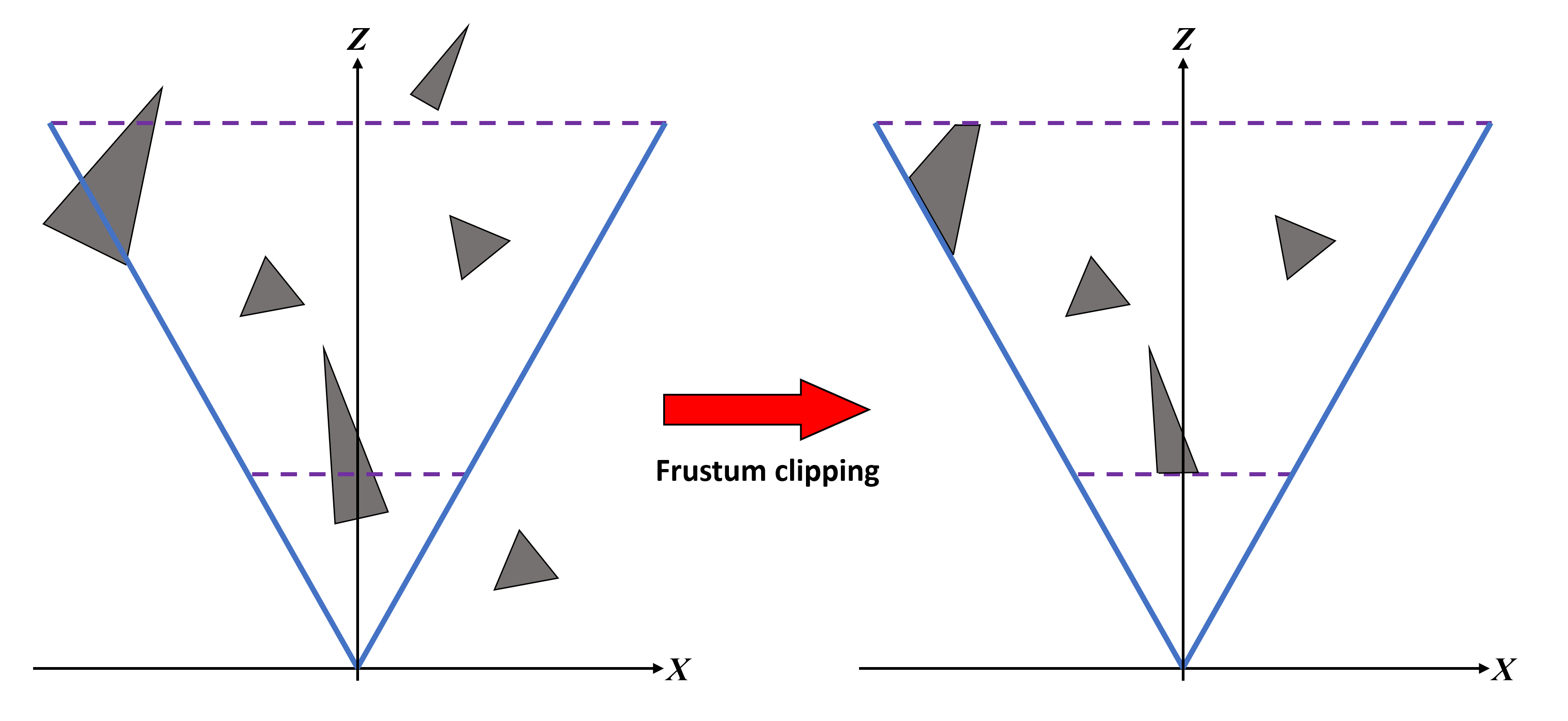
Il est à noter que la position du plan de découpage lointain n’est pas nécessairement la même que dessiner la distance dans les jeux, car ce dernier est contrôlé par le moteur de jeu lui-même. Quelque chose d'autre que le moteur va faire est élimination des déchets – c'est ici que le code est exécuté pour déterminer si un objet va se trouver dans le tronc et / ou affecter tout ce qui va être visible; si la réponse est non, alors cet objet n'est pas envoyé pour le rendu. Ce n'est pas la même chose que l'écrêtage de frustrum, car même si les primitives en dehors de frustrum sont supprimées, elles ont tout de même été traitées à l'étape du traitement des sommets. Avec l'abattage, ils ne sont pas traités du tout, ce qui permet d'économiser beaucoup de performances.
Maintenant que nous avons effectué toutes nos transformations et découpages, il semblerait que les sommets soient enfin prêts pour la prochaine étape de la séquence de rendu. Sauf qu'ils ne le sont pas. En effet, tous les calculs effectués dans le traitement des sommets et les opérations d’espace entre les découpages doivent être effectués avec un système de coordonnées homogène (c’est-à-dire que chaque sommet a 4 composants plutôt que 3). Cependant, la fenêtre de visualisation est entièrement en 2D et l’API attend donc que les informations de sommet aient uniquement des valeurs pour x, y (la valeur de la profondeur z est retenu cependant).
Pour se débarrasser du 4ème composant, un division en perspective est fait où chaque composant est divisé par le w valeur. Ce réglage verrouille la plage de valeurs X et y peut prendre à [-1,1] et z à la gamme de [0,1] – on les appelle coordonnées normalisées de l'appareil (NDC pour faire court).
Si vous souhaitez plus d'informations sur ce que nous venons de décrire et que vous souhaitez vous plonger dans beaucoup plus de mathématiques, alors lisez l'excellent tutoriel de Song Ho Ahn sur le sujet. Maintenant, transformons ces sommets en pixels!
Maîtriser ce raster
Comme pour les transformations, nous verrons comment Direct3D définit les règles et les processus permettant de transformer la fenêtre d'affichage en grille de pixels. Cette grille ressemble à une feuille de calcul, avec des lignes et des colonnes, chaque cellule contenant plusieurs valeurs de données (telles que la couleur, les valeurs de profondeur, les coordonnées de texture, etc.). En règle générale, cette grille est appelée un raster et le processus de génération est connu sous le nom rastérisation. Dans notre article sur le rendu 3D 101, nous avons présenté une vue très simplifiée de la procédure:
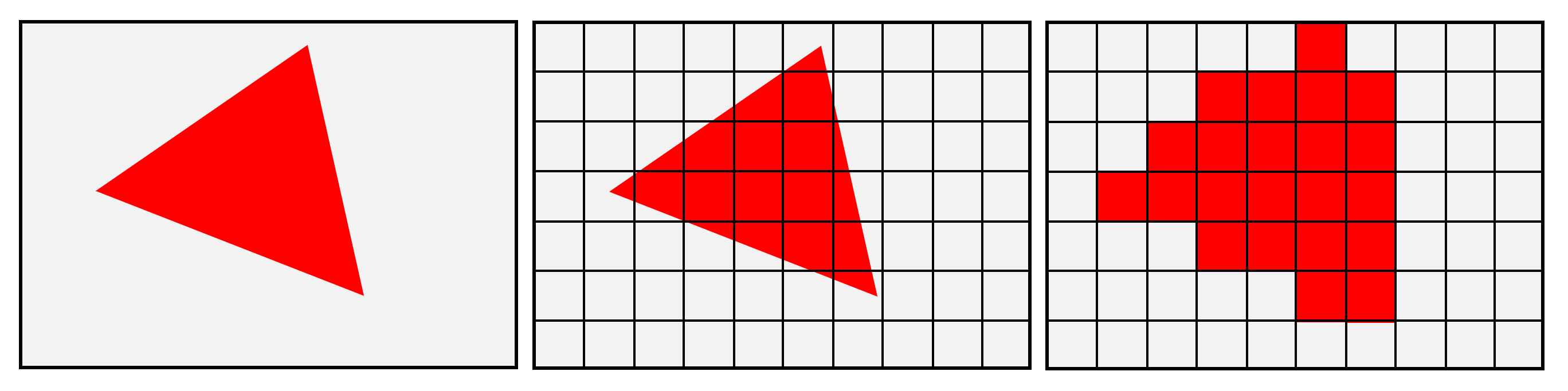
L'image ci-dessus donne l'impression que les primitives sont simplement découpées en petits blocs, mais il y a beaucoup plus que cela. La toute première étape consiste à déterminer si un primitif fait face à la caméra – dans une image plus haut dans cet article, celle qui montre le frustrum, les primitives constituant le dos du lapin gris, par exemple, ne le seraient pas. Être visible. Ainsi, bien qu'ils soient présents dans la fenêtre d'affichage, il n'est pas nécessaire de les restituer.
Nous pouvons avoir une idée approximative de ce à quoi cela ressemble avec le diagramme suivant. Le cube a subi diverses transformations pour placer le modèle 3D dans un espace d'écran 2D et, du point de vue de la caméra, plusieurs faces du cube ne sont pas visibles. Si nous supposons qu'aucune des surfaces n'est transparente, plusieurs de ces primitives peuvent être ignorées.
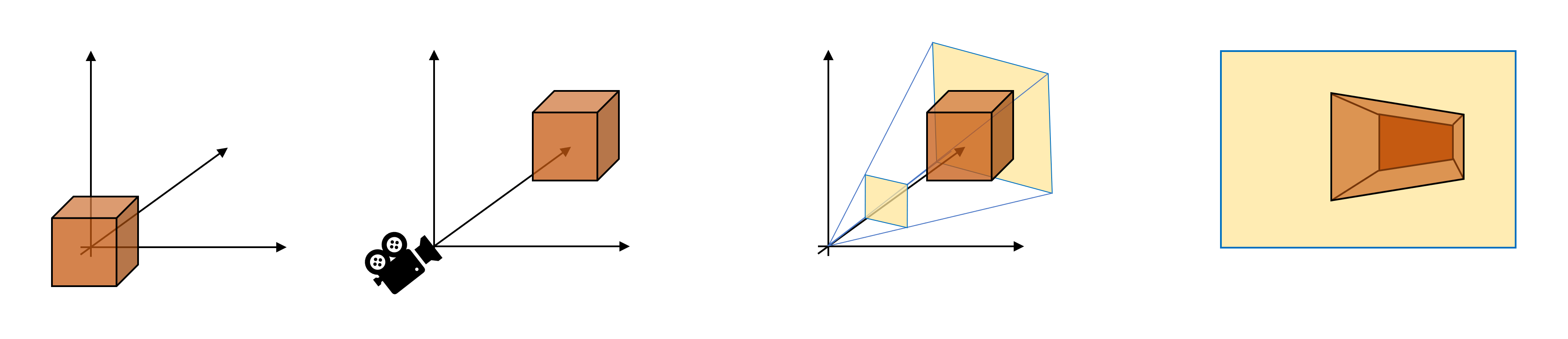
Dans Direct3D, cela peut être réalisé en indiquant au système ce que le rendre l'état va être, et cette instruction lui dira de supprimer (aka cueillirb) face à chaque primitive (ou à ne pas éliminer du tout – par exemple, si fil de fer mode). Mais comment sait-il ce qui est devant ou derrière? Lorsque nous avons examiné les calculs mathématiques dans le traitement des sommets, nous avons constaté que les triangles (ou plutôt le cas des sommets) ont des vecteurs normaux qui indiquent au système son orientation. Avec cette information, une vérification simple peut être effectuée et si la primitive échoue, elle est supprimée de la chaîne de rendu.
Ensuite, il est temps de commencer à appliquer la grille de pixels. Encore une fois, cela est étonnamment complexe, car le système doit déterminer si un pixel convient à une primitive – complètement, partiellement ou pas du tout. Pour ce faire, un processus appelé test de couverture est fait. L'image ci-dessous montre comment les triangles sont rasterisés dans Direct3D 11:
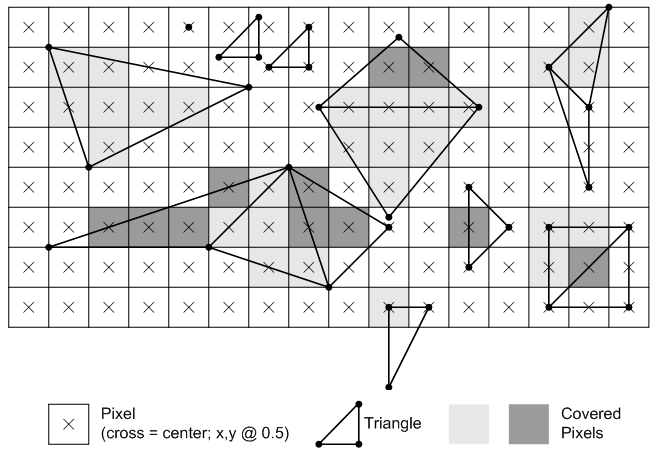
La règle est assez simple: un pixel est réputé être à l'intérieur d'un triangle si le centre du pixel passe ce que Microsoft appelle la règle «en haut à gauche». La partie "supérieure" est une vérification de ligne horizontale; le centre de pixel doit être sur cette ligne. La partie "gauche" correspond aux lignes non horizontales et le centre du pixel doit se trouver à gauche de cette ligne. Il existe des règles supplémentaires pour les non-primitives, c’est-à-dire des lignes et des points simples, et les règles gagnent des conditions supplémentaires si multi-échantillonnage Est employé.
Si nous examinons attentivement l'image de la documentation de Microsoft, nous constatons que les formes créées par les pixels ne ressemblent pas beaucoup aux primitives d'origine. En effet, les pixels sont trop volumineux pour créer un triangle réaliste. Le raster contient des données insuffisantes sur les objets d'origine, ce qui entraîne un problème appelé aliasing.
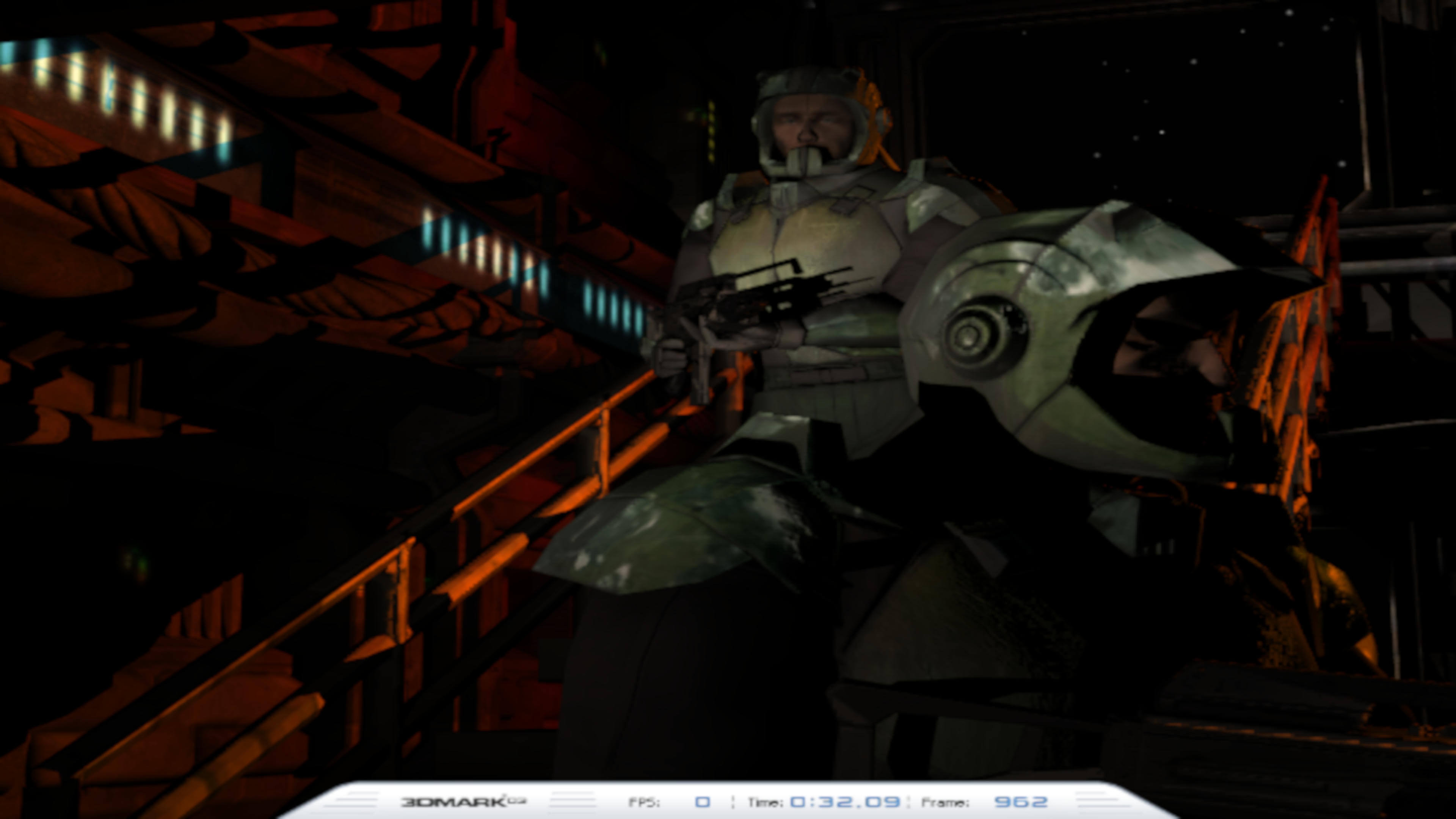
Utilisons 3DMark03 d'UL Benchmark pour voir le repliement du spectre:
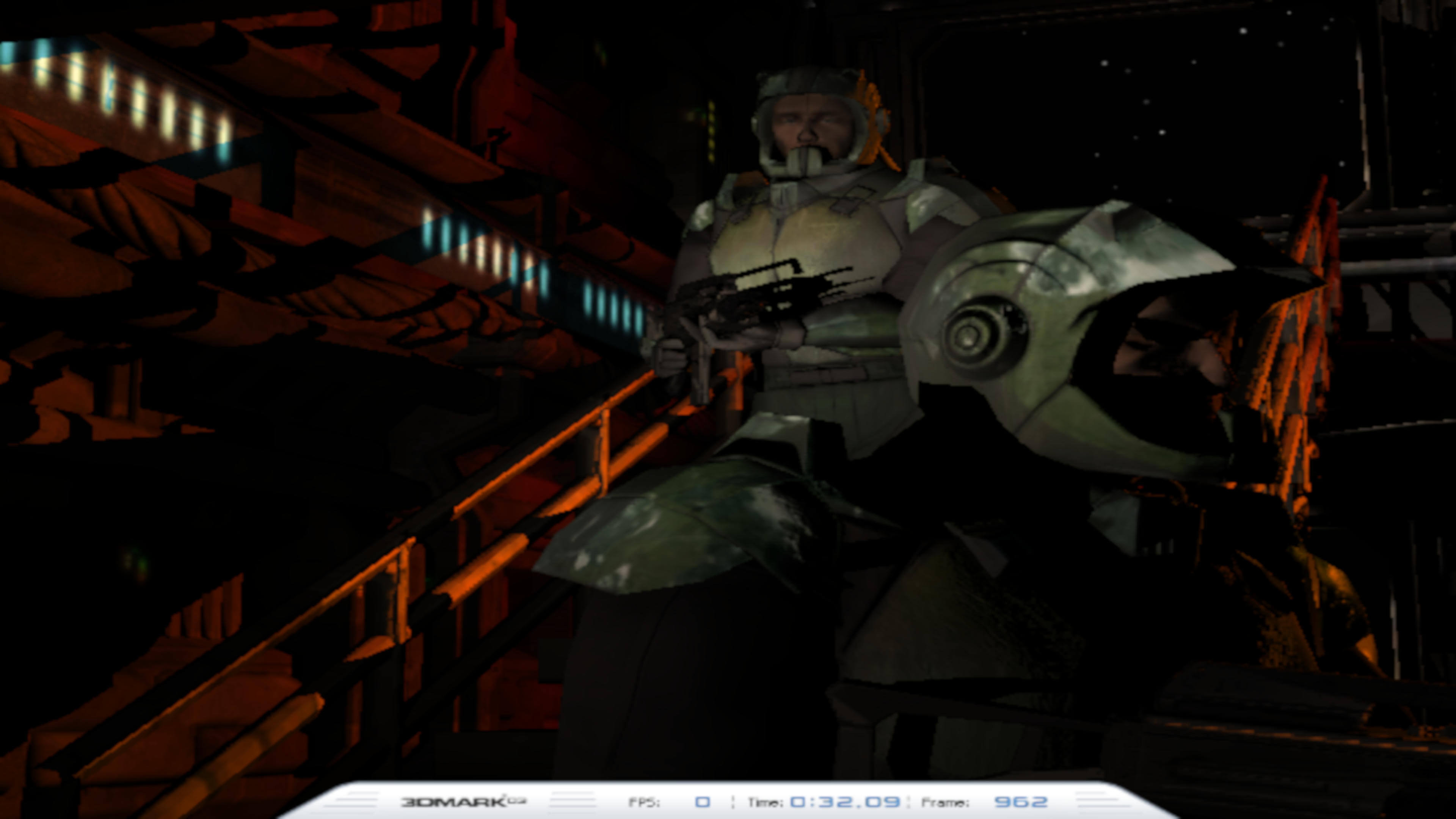
Dans la première image, la taille du raster était très basse (720 x 480 pixels). Le pseudonyme peut être clairement vu sur la main courante et l'ombre jette le pistolet détenu par le soldat supérieur. Comparez cela à ce que vous obtenez avec un raster qui a 24 fois plus de pixels:
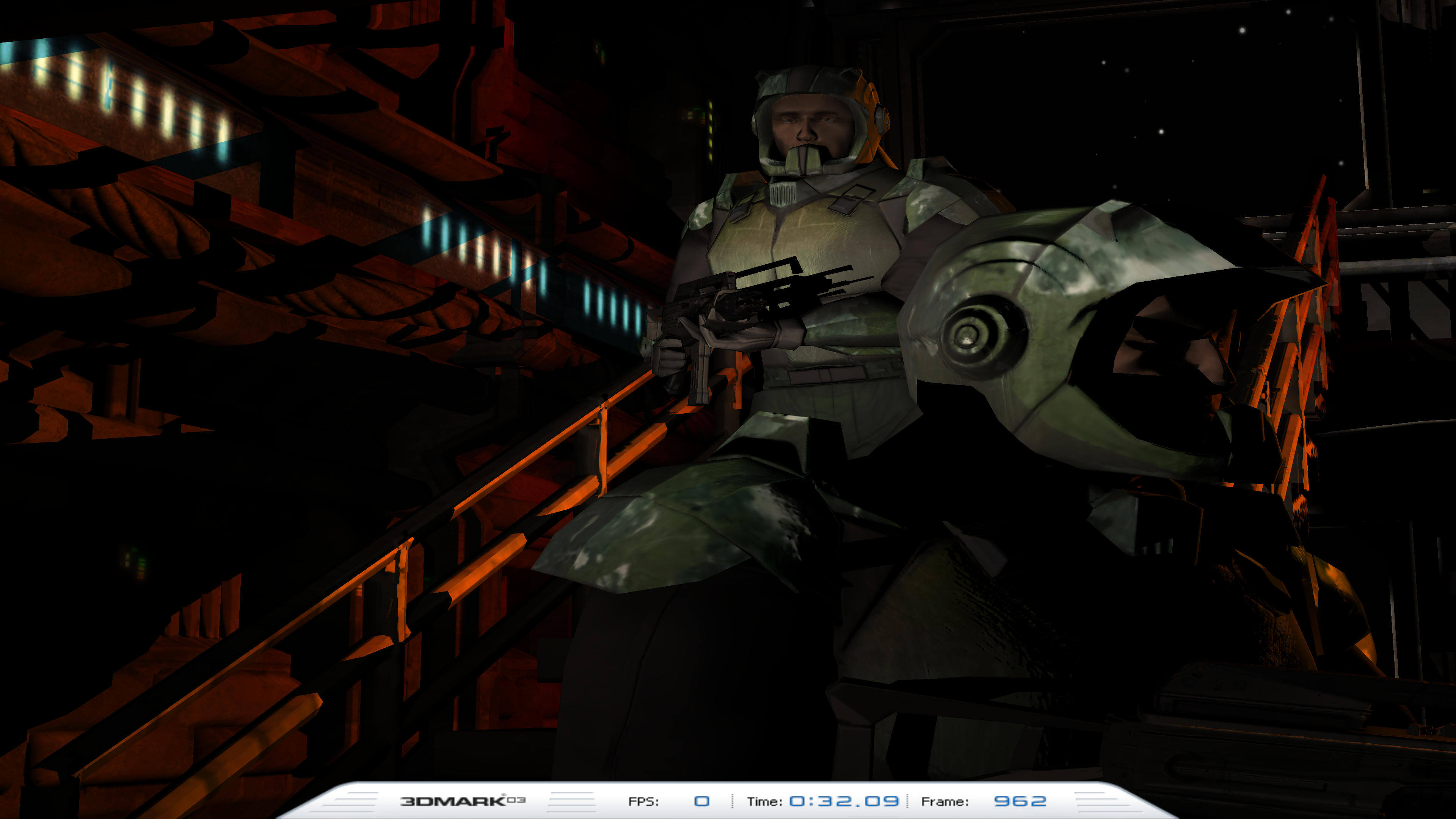
Ici, nous pouvons voir que le pseudonyme sur la main courante et l’ombre a complètement disparu. Un plus grand raster semble être le chemin à parcourir à chaque fois mais les dimensions de la grille doivent être supportées par le moniteur sur lequel le cadre sera affiché et étant donné que ces pixels doivent être traités, après le processus de rastérisation, être une pénalité de performance évidente.
Le multi-échantillonnage peut vous aider et voici comment cela fonctionne dans Direct3D:
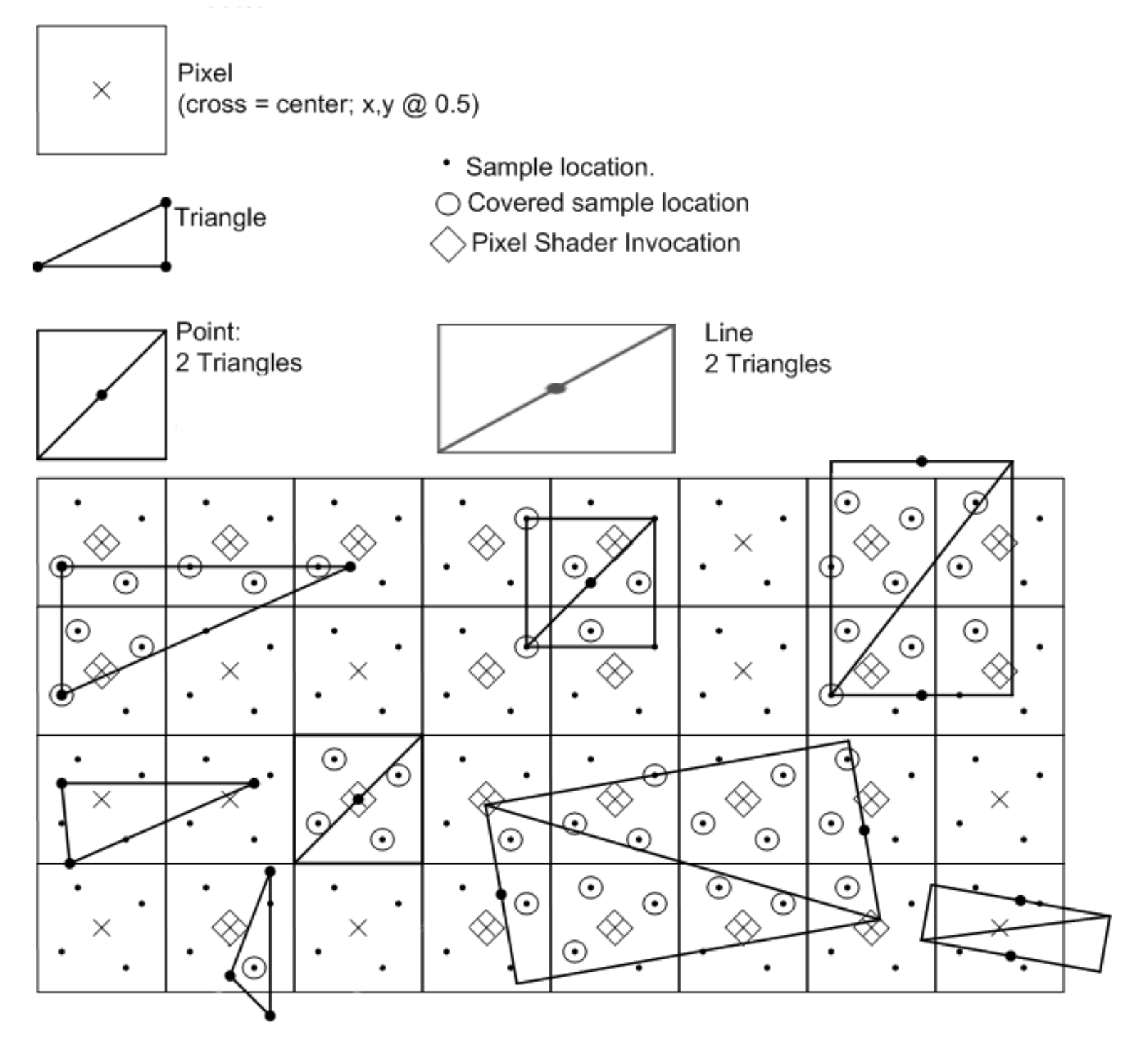
Plutôt que de simplement vérifier si un centre de pixels respecte les règles de rastérisation, plusieurs emplacements (appelés exemples de sous-pixels ou sous-échantillons) au sein de chaque pixel sont testés à la place, et si l’un d’eux est correct, alors ce pixel entier fait partie de la forme. Cela peut sembler n'avoir aucun avantage et peut-être même aggraver le repliement du spectre, mais lorsque le multi-échantillonnage est utilisé, les informations sur les sous-échantillons couverts par la primitive et les résultats du traitement des pixels sont stockés dans une mémoire tampon.
Ce tampon est ensuite utilisé pour mélanger les données de sous-échantillon et de pixel de manière à ce que les bords de la primitive soient moins encombrants. Nous reviendrons sur la situation des alias dans un article ultérieur, mais pour l’instant, c’est ce que le multi-échantillonnage peut faire lorsqu’il est utilisé sur un raster avec trop peu de pixels:
Nous pouvons voir que la quantité de repliement sur les bords des différentes formes a été considérablement réduite. Un raster plus volumineux est certainement meilleur, mais le résultat en termes de performances peut plutôt favoriser l'utilisation du multi-échantillonnage.
Quelque chose d'autre qui peut être fait dans le processus de rastérisation est test d'occlusion. Cela doit être fait car la fenêtre de visualisation sera pleine de primitives qui se chevaucheront (occlus) – par exemple, dans l’image ci-dessus, les triangles faisant face au devant qui composent le soldat au premier plan chevauchent les mêmes triangles que l’autre soldat. En plus de vérifier si une primitive couvre un pixel, les profondeurs relatives peuvent également être comparées et si l'une est derrière l'autre, elle pourrait être ignorée du reste du processus de rendu.
Toutefois, si la primitive proche est transparente, la primitive restante sera toujours visible, même si la vérification de l'occlusion a échoué. C’est pourquoi presque tous les moteurs 3D effectuent des contrôles d’occlusion. avant envoyer quelque chose au GPU et crée à la place quelque chose appelé un tampon z dans le cadre du processus de rendu. C'est ici que le cadre est créé normalement, mais au lieu de stocker les couleurs de pixel finales en mémoire, le GPU ne stocke que les valeurs de profondeur. Ceci peut ensuite être utilisé dans les shaders pour vérifier la visibilité avec davantage de contrôle et de précision sur les aspects impliquant le chevauchement d'objets.

Dans l'image ci-dessus, plus la couleur du pixel est sombre, plus l'objet est proche de la caméra. La trame est rendue une fois, pour créer le tampon z, puis à nouveau, mais cette fois, lorsque les pixels sont traités, un shader est exécuté pour les comparer aux valeurs du tampon z. Si ce n'est pas visible, alors cette couleur de pixel n'est pas mise dans le tampon d'image final.
Pour l'instant, la dernière étape consiste à faire interpolation d'attribut de sommet – dans notre schéma simplifié initial, la primitive était un triangle complet, mais n'oubliez pas que la fenêtre d'affichage est simplement remplie avec les coins des formes, pas la forme elle-même. Le système doit donc déterminer la couleur, la profondeur et la texture de la primitive entre les sommets. interpolation. Comme vous pouvez l'imaginer, ceci est un autre calcul, et non un calcul simple non plus.
Bien que l'écran tramé soit en 2D, les structures qu'il contient représentent une perspective 3D forcée. Si les lignes étaient vraiment 2 dimensions, alors nous pourrions utiliser un simple linéaire équation pour élaborer les différentes couleurs, etc. au fur et à mesure que nous passons d’un sommet à un autre. Mais à cause de l'aspect 3D de la scène, l'interpolation doit tenir compte de la perspective – lisez le superbe blog de Simon Yeung sur le sujet pour obtenir plus d'informations sur le processus.
Nous y voilà. Ainsi, un monde 3D de sommets devient une grille 2D de blocs colorés. Nous n'avons pas encore terminé.
Tout est à l'envers (sauf quand ça ne l'est pas)
Avant de terminer notre étude de la pixellisation, nous devons dire quelque chose sur l'ordre de la séquence de rendu. Nous ne parlons pas de l'endroit où, par exemple, la tessellation vient dans la séquence; au lieu de cela, nous faisons référence à l'ordre dans lequel les primitives sont traitées. Les objets sont généralement traités dans l'ordre dans lequel ils apparaissent dans le tampon d'index (le bloc de mémoire qui indique au système comment les sommets sont regroupés), ce qui peut avoir un impact significatif sur la gestion des objets et des effets transparents.
La raison en est que les primitives sont gérées une à la fois et que si vous calculez d’abord celles du premier, celles qui se trouvent derrière ne seront pas visibles (c’est là que l’abattage par occlusion entre vraiment en jeu). et peut être supprimé du processus (aider la performance) – on l’appelle généralement 'avant vers l'arrière' rendu et nécessite que le tampon d'index soit commandé de cette manière.
Cependant, si certaines de ces primitives situées devant la caméra sont transparentes, le rendu avant-arrière aurait pour conséquence que les objets situés derrière l'élément transparent seraient omis. Une solution consiste à tout restituer à l'envers, les primitives transparentes et les effets étant exécutés en dernier.
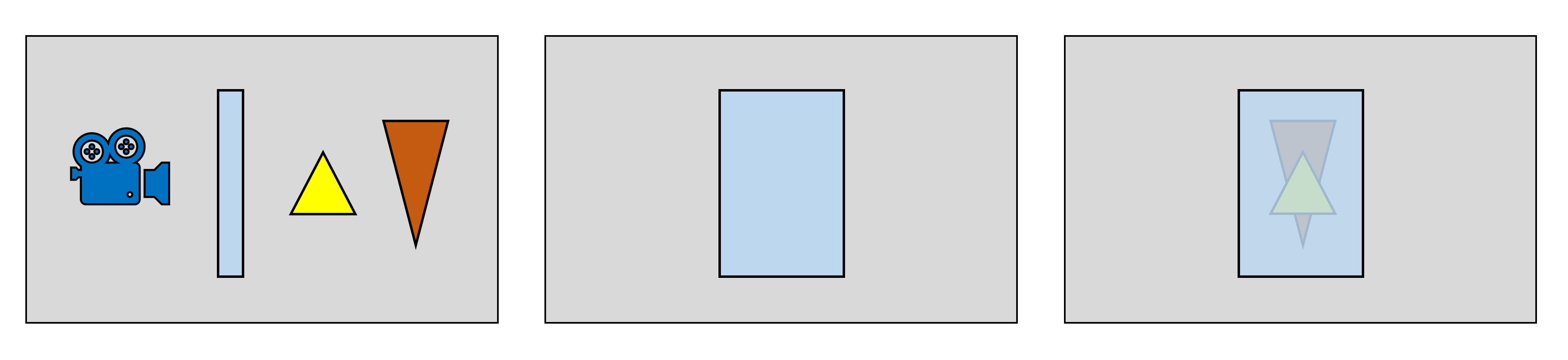
Donc, tous les jeux modernes font un rendu arrière, oui? Pas si cela peut être aidé – n'oubliez pas que le rendu de chaque primitive aura un coût de performance beaucoup plus élevé que celui de rendre visible uniquement celles qui peuvent être vues. Il existe d'autres méthodes de traitement des objets transparents, mais en règle générale, il n'existe pas de solution unique et chaque situation doit être traitée de manière unique.
Cela résume essentiellement les avantages et les inconvénients de la pixellisation – sur du matériel moderne, c’est vraiment rapide et efficace, mais cela reste une approximation de ce que nous voyons. Dans le monde réel, chaque objet absorbera, réfléchira et peut-être réfractera la lumière, ce qui affectera la scène visualisée. En divisant le monde en primitives et en ne rendant que certaines d'entre elles, nous obtenons un résultat rapide mais approximatif.
Si seulement il y avait un autre moyen …
Là est une autre façon: le traçage des rayons
Il y a près de cinq décennies, un chercheur en informatique, Arthur Appel, a mis au point un système permettant de rendre des images sur un ordinateur, selon lequel un seul rayon de lumière était projeté en ligne droite à partir de la caméra, jusqu'à ce qu'il heurte un objet. À partir de là, les propriétés du matériau (sa couleur, sa réflectivité, etc.) modifieraient alors l'intensité du rayon lumineux. Chaque pixel de l'image rendue aurait une distribution de rayon et un algorithme serait exécuté, en passant par une séquence mathématique pour déterminer la couleur du pixel. Le processus d'Appel est devenu connu sous le nom de lancer de rayons.
Environ 10 ans plus tard, un autre scientifique, John Whitt, développa un algorithme mathématique qui faisait la même chose que l'approche d'Appel, mais lorsque le rayon frappait un objet, il générait des rayons supplémentaires, qui se déclenchaient dans différentes directions en fonction du matériau de l'objet. Parce que ce système générerait de nouveaux rayons pour chaque interaction d'objet, l'algorithme était de nature récursive et était donc beaucoup plus difficile en calcul; Cependant, elle présentait un avantage significatif par rapport à la méthode d'Appel, car elle pouvait correctement prendre en compte les réflexions, la réfraction et les ombres. Le nom de cette procédure était tracé laser (à proprement parler, c'est en arrière le traçage des rayons, lorsque nous suivons le rayon depuis la caméra et non depuis les objets) et qu’il est depuis lors le Saint Graal pour l’infographie et les films.
Le nom de cette procédure s'appelait traçage de rayons (à proprement parler, c’est le traçage de rayons en arrière, car nous suivons le rayon depuis la caméra et non depuis les objets) et c’est depuis lors le Saint-Graal des graphiques et des films.
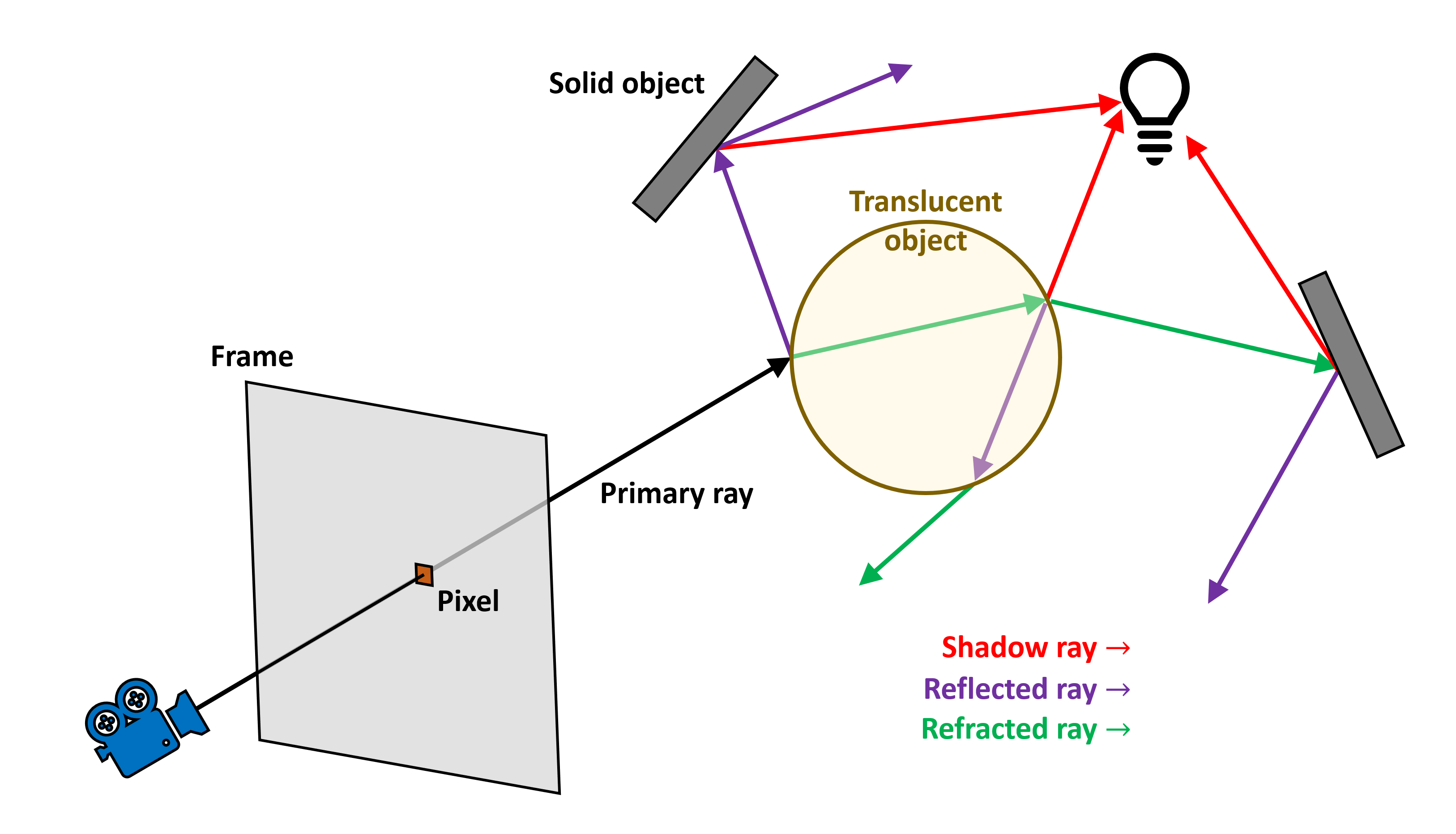
Dans l'image ci-dessus, nous pouvons avoir une idée du fonctionnement de l'algorithme de Whitted. Un rayon est lancé à partir de la caméra, pour chaque pixel du cadre, et se déplace jusqu'à atteindre une surface. Cette surface particulière est translucide, donc la lumière va se refléter et se réfracter à travers elle. Les rayons secondaires sont générés dans les deux cas et se propagent jusqu'à ce qu'ils interagissent avec une surface. Il existe également des sources secondaires, permettant de prendre en compte la couleur des sources de lumière et les ombres qu’elles génèrent.
La partie récursive du processus est que des rayons secondaires peuvent être générés chaque fois qu'un rayon nouvellement lancé intersecte une surface. Cela pourrait facilement devenir incontrôlable, de sorte que le nombre de rayons secondaires générés est toujours limité. Une fois le trajet des rayons terminé, sa couleur à chaque point terminal est calculée en fonction des propriétés matérielles de cette surface. Cette valeur est ensuite transmise du rayon précédent au précédent, en ajustant la couleur pour cette surface, et ainsi de suite, jusqu'à atteindre le point de départ effectif du rayon principal: le pixel dans le cadre.
Cela peut être extrêmement complexe et même des scénarios simples peuvent générer une multitude de calculs. Heureusement, certaines solutions peuvent être utiles, notamment l’utilisation de matériel spécifiquement conçu pour accélérer ces opérations mathématiques, comme pour le calcul matriciel dans le traitement des sommets (plus à ce sujet dans un instant). ). Un autre point critique est d’essayer d’accélérer le processus effectué pour déterminer quel objet est frappé par un rayon et à quel endroit exactement sur la surface de l’objet où se croise l’intersection – si l’objet est constitué de beaucoup de triangles, cela peut être surprenant. difficile à faire:

Plutôt que de tester chaque triangle, dans chaque objet, une liste de volumes englobants (BV) est générée avant le lancer de rayon – il s’agit simplement de cuboïdes qui entourent l’objet en question, les plus petits générés successivement pour les différentes structures à l’intérieur. L'object.
Par exemple, le premier BV serait pour le lapin entier. Le couple suivant couvrirait sa tête, ses jambes, son torse, sa queue, etc. chacun d'entre eux serait alors une autre collection de volumes pour les plus petites structures de la tête, etc., le niveau final des volumes contenant un petit nombre de triangles à tester. Tous ces volumes sont ensuite rangés dans une liste ordonnée (appelée une Hiérarchie BV ou BVH en abrégé), de sorte que le système vérifie chaque fois un nombre relativement petit de BV:
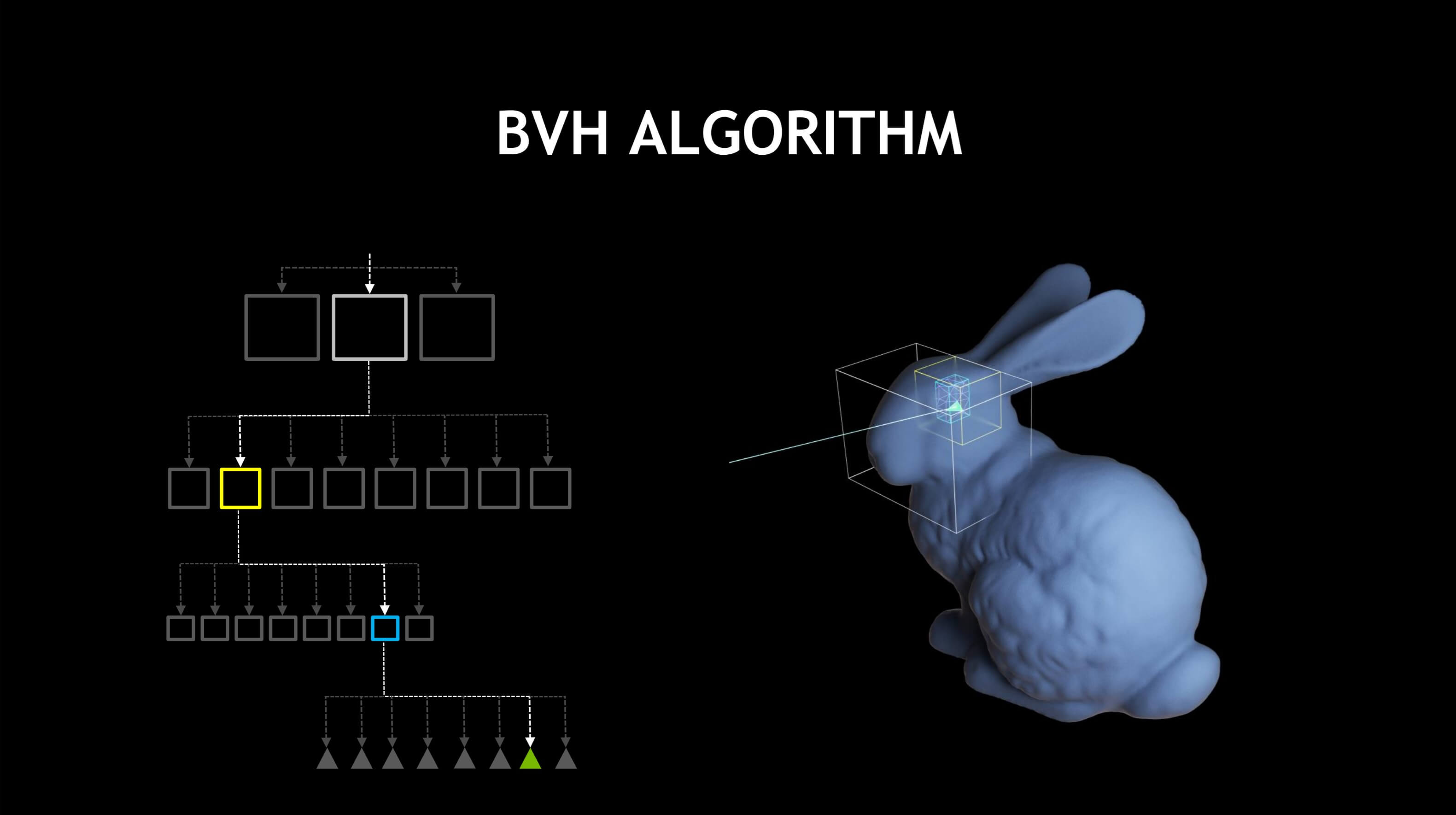
Bien que l'utilisation d'un BVH n'accélère pas techniquement le traçage de rayon proprement dit, la génération de la hiérarchie et l'algorithme de recherche nécessaire sont généralement beaucoup plus rapides que de devoir vérifier si un rayon croise un million de triangles. dans un monde en 3D.
Aujourd'hui, des programmes tels que Blender et POV-ray utilisent le traçage de rayons avec des algorithmes supplémentaires (tels que le traçage de photons et la radiosité) pour générer des images très réalistes:

La question évidente à poser est de savoir si le lancer de rayons est si bon, pourquoi ne l'utilisons-nous pas partout? Les réponses se situent dans deux domaines: tout d’abord, même le simple lancer de rayons génère des millions de rayons qui doivent être calculés à plusieurs reprises. Le système commence avec un seul rayon par pixel d'écran, soit une résolution de 800 x 600 pixels, qui génère 480 000 rayons primaires, puis chacun génère plusieurs rayons secondaires. C'est un travail vraiment difficile pour les ordinateurs de bureau actuels. Le deuxième problème est que le tracé de rayons de base n’est pas vraiment réaliste et qu’il faut inclure toute une série d’équations très complexes pour obtenir les résultats escomptés.
Même avec du matériel informatique moderne, la quantité de travail requise dépasse le cadre requis pour le faire en temps réel pour un jeu en 3D actuel. Dans notre article sur le rendu 3D 101, nous avons vu dans un repère de traçage de rayons qu'il fallait des dizaines de secondes pour produire une seule image en basse résolution.
Alors, comment le Wolfenstein 3D original faisait-il du lancer des rayons depuis 1992, et pourquoi Battlefield V et Metro Exodus, tous deux publiés en 2019, offrent-ils des fonctionnalités de traçage des rayons? Sont-ils en train de rasteriser ou de lancer de rayons? La réponse est: un peu des deux.
L'approche hybride pour le présent et l'avenir
En mars 2018, Microsoft a annoncé une nouvelle extension d'API pour Direct3D 12, appelée DXR (DirectX Raytracing). Il s’agissait d’un nouveau pipeline graphique, destiné à compléter les pipelines de calcul standard et de calcul. Les fonctionnalités supplémentaires ont été fournies via l'introduction des shaders, des structures de données, etc., mais ne nécessitent aucun support matériel spécifique, à l'exception de celui déjà requis pour Direct3D 12.

Lors de la même conférence des développeurs de jeux, où Microsoft a parlé de DXR, Electronic Arts a parlé de son projet Pica Pica, une expérience de moteur 3D utilisant DXR. Ils ont montré que le lancer de rayons peut être utilisé, mais pas pour le rendu complet. Au lieu de cela, les techniques traditionnelles de pixellisation et de calcul seraient utilisées pour la majeure partie du travail, DXR étant utilisé pour des zones spécifiques. Cela signifie que le nombre de rayons générés est bien inférieur à celui d'une scène entière.

Cette approche hybride avait été utilisée dans le passé, mais dans une moindre mesure. Par exemple, Wolfenstein 3D a utilisé la diffusion de rayons pour déterminer l’apparence de l’image rendue, bien que cela ait été fait avec un rayon par colonne de pixels plutôt que par pixel. Cela peut encore sembler très impressionnant, jusqu'à ce que vous réalisiez que le jeu fonctionnait à l'origine avec une résolution de 640 x 480, de sorte que pas plus de 640 rayons ne fonctionnaient jamais en même temps.
La carte graphique du début de 2018, comme la Radeon RX 580 d’AMD ou la GeForce 1080 Ti de Nvidia, répondait certainement à la configuration matérielle requise pour le DXR, mais même avec ses capacités de calcul, il était peu probable qu’il soit suffisamment puissant pour utiliser DXR. de manière significative.
Cela a quelque peu changé en août 2018, lorsque Nvidia a lancé sa toute dernière architecture GPU, Turing, nom de code. La caractéristique essentielle de cette puce a été l’introduction de ce qu’on appelle les «RT Cœurs»: unités logiques dédiées pour accélérer les calculs de croisement intersection rayon-triangle et de hiérarchie des volumes (BVH). Ces deux processus sont des routines chronophages permettant de déterminer l’interaction d’une lumière avec les triangles qui composent divers objets d’une scène. Étant donné que les cœurs RT étaient uniques pour le processeur Turing, leur accès ne pouvait être effectué que via l'API propriétaire de Nvidia.
Battlefield V d'EA a été le premier jeu à prendre en charge cette fonctionnalité. Lorsque nous avons testé l'utilisation de DXR, nous avons été impressionnés par les améliorations apportées aux réflexions sur l'eau, le verre et le métal dans le jeu.
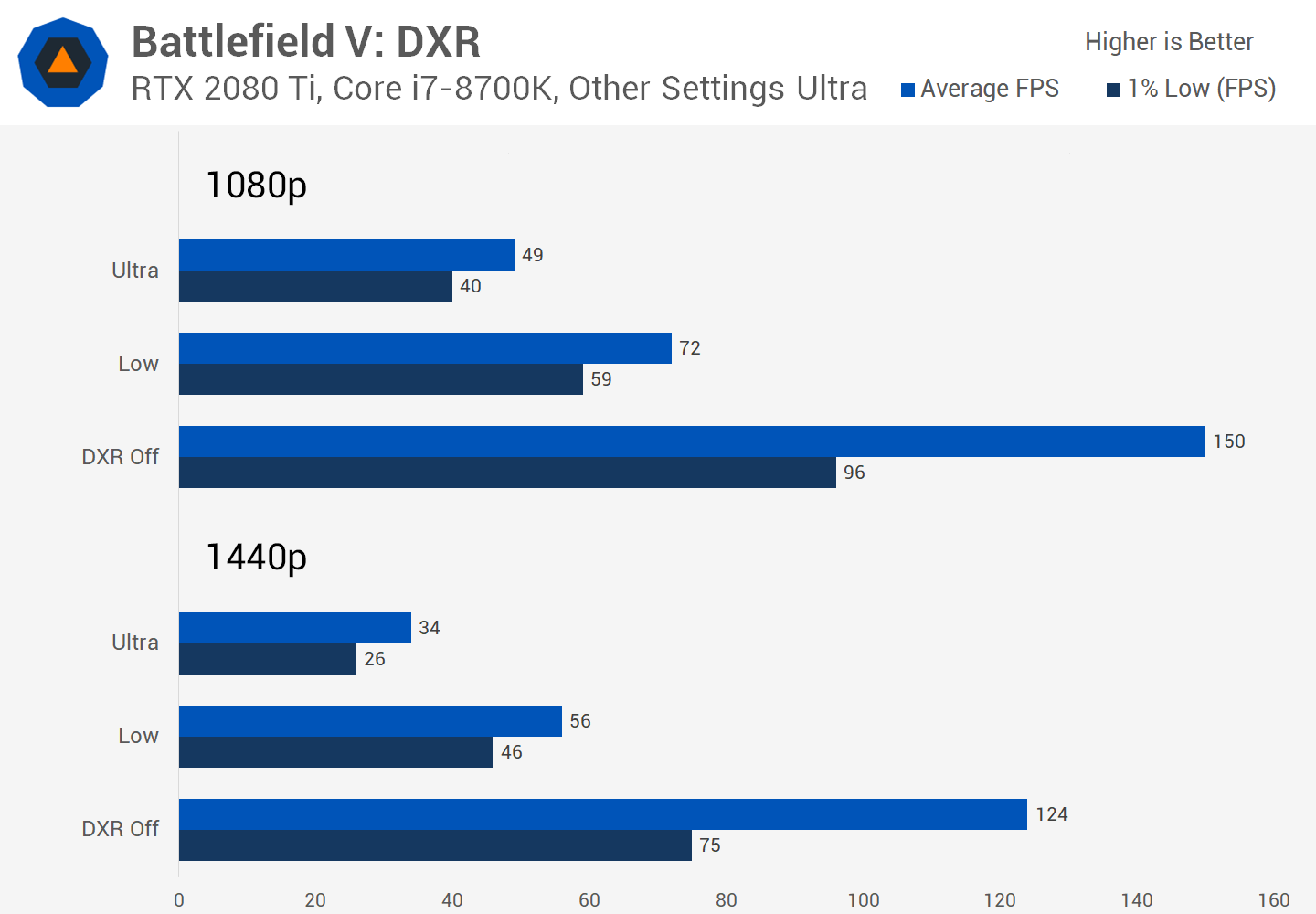
Pour être honnête, les correctifs ultérieurs ont quelque peu amélioré les choses, mais il y avait (et est toujours) une grosse baisse de la vitesse à laquelle les images étaient rendues. En 2019, d'autres jeux apparaissaient, qui prenaient en charge cette API, effectuant le lancer de rayons pour des pièces spécifiques dans une image. Nous avons testé Metro Exodus et Shadow of the Tomb Raider, et nous avons trouvé un scénario similaire: dans le cas d’une utilisation intensive, DXR affecterait considérablement le taux de trame.
À peu près au même moment, UL Benchmarks a annoncé un test de fonctionnalité DXR pour 3DMark:

Cependant, notre examen des jeux compatibles DXR et le test de fonctionnalité de 3DMark ont prouvé que le traçage des rayons était une chose certaine: en 2019, le processeur graphique était encore très dur, même pour les modèles à plus de 1 000 $. Cela signifie-t-il que nous n'avons pas de réelle alternative à la pixellisation?
Les fonctionnalités de pointe de la technologie graphique 3D grand public sont souvent très onéreuses et la prise en charge initiale des nouvelles fonctionnalités d'API peut être assez inégale ou lente (comme nous l'avons constaté lorsque nous avons testé Max Payne 3 sur une gamme de versions de Direct3D vers 2012), cette dernière Cela est généralement dû au fait que les développeurs de jeux tentent d’inclure autant de fonctionnalités améliorées que possible, parfois avec une expérience limitée.
Mais là où les shaders de vertex et de pixel, la tesselation, le rendu HDR et l’occlusion ambiante de l’écran étaient autrefois très exigeants et ne convenaient qu’aux GPU haut de gamme, leur utilisation est désormais courante dans les jeux et est prise en charge par une large gamme de cartes graphiques. Il en ira de même pour le lancer de rayon et compte tenu du temps, il deviendra simplement un autre paramètre de détail qui sera activé par défaut pour la plupart des utilisateurs.
Quelques réflexions finales
Nous arrivons ainsi à la fin de notre deuxième plongée en profondeur, au cours de laquelle nous avons examiné de plus près le monde des graphiques 3D. Nous avons vu comment les sommets des modèles et des mondes sont déplacés de 3 dimensions et transformés en une image 2D plate. Nous avons vu comment les paramètres de champ de vision doivent être pris en compte et quel effet ils produisent. Le processus de transformation de ces sommets en pixels a été exploré et nous avons terminé par un bref aperçu d’un processus alternatif à la pixellisation.
Comme auparavant, nous n’aurions pas pu tout couvrir et avoir passé sous silence quelques détails ici et là – après tout, ce n’est pas un manuel! Mais nous espérons que vous avez acquis un peu plus de connaissances en cours de route et que vous avez une nouvelle admiration pour les programmeurs et les ingénieurs qui maîtrisent vraiment les mathématiques et les sciences nécessaires pour que tout cela se produise dans vos titres 3D préférés.
Nous serons plus qu'heureux de répondre à vos questions, alors n'hésitez pas à les envoyer dans la section commentaires. Jusqu'au prochain.
Masthead credit: Monochrome printing raster abstract by Aleksei Derin
